هل شاهدت الفيديو الذي يقوم فيه ذراع الروبوت بتسديد كرة البولينغ؟ تبيّن أنه مزيُف تماماً

انتشر منذ بضعة أيام فيديو لذراع روبوت وهو يقوم بتسديد كرة البولينغ، وكان هذا الفيديو رائعاً وحصل على عدد كبير من المشاهدات. لكن إذا نظرنا إلى الفيديو من ناحية علمية، وتحديداً من ناحية فيزيائية، فسيتبين لنا أن الأمر ليس تماماً كما يبدو.

شاهد هذا الفيديو الذي يقوم فيه الروبوت بتسديد الكرة أولاً، ثم تابع معنا هذه المقالة لتتعرف على حقيقة الموضوع:

وكما قرأت في عنوان هذه المقالة، فالقصة بأكملها محض خدعة، وإليكم التفاصيل.

حركة الكرة في الهواء

تنطلق الكرة من ذراع الروبوت لتصل إلى القطع الخشبية بدون أن تضرب أو تصطدم بالأرض، وبعد أن تنطلق الكرة من الذراع، فلا تعيقها أي مقاومة سوى قوة الجاذبية التي تسحبها للأسفل (باعتبار أن مقاومة الهواء مهملة). وتلك الحركة مشابهة جداً لحركة القذيفة التي تعلمناها في المدرسة، فبالإمكان دراسة حركة الكرة الرأسية والأفقية كل على حدا.

لا توجد أي قوة أفقية تؤثر على حركة الكرة بعد أن تغادر ذراع الروبوت، لذا ستكون سرعتها الأفقية ثابتة. أما في الاتجاه العمودي، فتنطلق الكرة بسرعة رأسية مقدراها صفر، ثم تبدأ بالتسارع بمقدار 9.8 متر في الثانية (قوة الجاذبية).

فإذا انطلقت الكرة أفقياً (أو هكذا تبدو على الأقل)، نستطيع حساب سرعة انطلاقها بحساب الزمن الذي تستغرقه الكرة للوصول إلى القطع الخشبية. وبما أنها تتحرك بسرعة، فهناك أداة لتحليل الفيديو تدعى Tracker Video Analysis، تتيح لنا معرفة الزمن الذي تستغرقه الكرة للوصول إلى القطع الخشبية والاصطدام بها. وهذا رابط الأداة:

يتبين لنا بعد الحساب أن الكرة تستغرق زمناً قدره 0.767 ثانية للانتقال عبر مضمار البولينغ والوصول إلى القطع، قاطعة بذلك مسافة قدرها 18.29 متر. وبالتالي نستطيع حساب السرعة الأفقية من القانون التالي (السرعة=المسافة/الزمن):

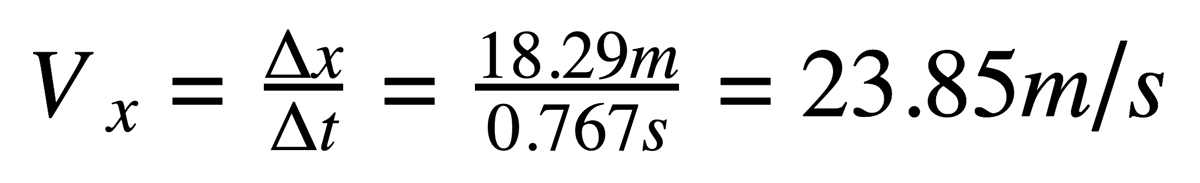
نجد أن سرعة قذف الكرة هي 23.85 متر في الثانية، وذلك في حالة قذفها بدون مركبة السرعة الرأسية.

وإذا أدخلنا الاتجاه الرأسي في الحساب، سنجد أن الكرة تسقط بنفس الزمن اللازم لوصولها إلى نهاية المضمار.

وباعتبار أننا حسبنا مسبقاً الزمن والتسارع، نستطيع إذاً حساب السرعة الرأسية كالتالي:

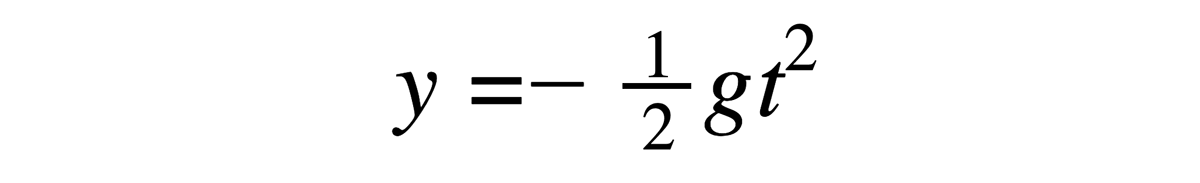
إذا أسقطنا الحركة على محاور الإحداثيات، سنلاحظ أن الكرة في نقطة الانطلاق (على المحور y) لم تقطع أي مسافة، وكذلك تكون سرعتها الرأسية مساوية للصفر، وباعتبار أن تسارع الجاذبية يساوي 9.8 متر بالثانية، وارتفاع الكرة عن الأرض يساوي 2.88 متر، لذا من غير الممكن إطلاق الكرة أفقياً بتلك السرعة ووصولها إلى نهاية المضمار والاصطدام بالقطع الخشبية بدون أن تصطدم بالأرض أولاً. فإما أن تُطلق بسرعة أكبر أو تطلق بزاوية أخرى (ألا تكون الزاوية صفر).

حركة الذراع

حسبنا مسبقاً سرعة إطلاق الكرة عن طريق حساب الزمن الذي تستغرقه للوصول إلى نهاية المضمار. لكن ماذا عن معدل دوران ذراع الروبوت؟ دعنا نقيسه!

سنستخدم مجدداً أداة تحليل الفيديو لمعرفة الزمن الذي تستغرقه الذراع في دورانها، وهذا ما حصلنا عليه:

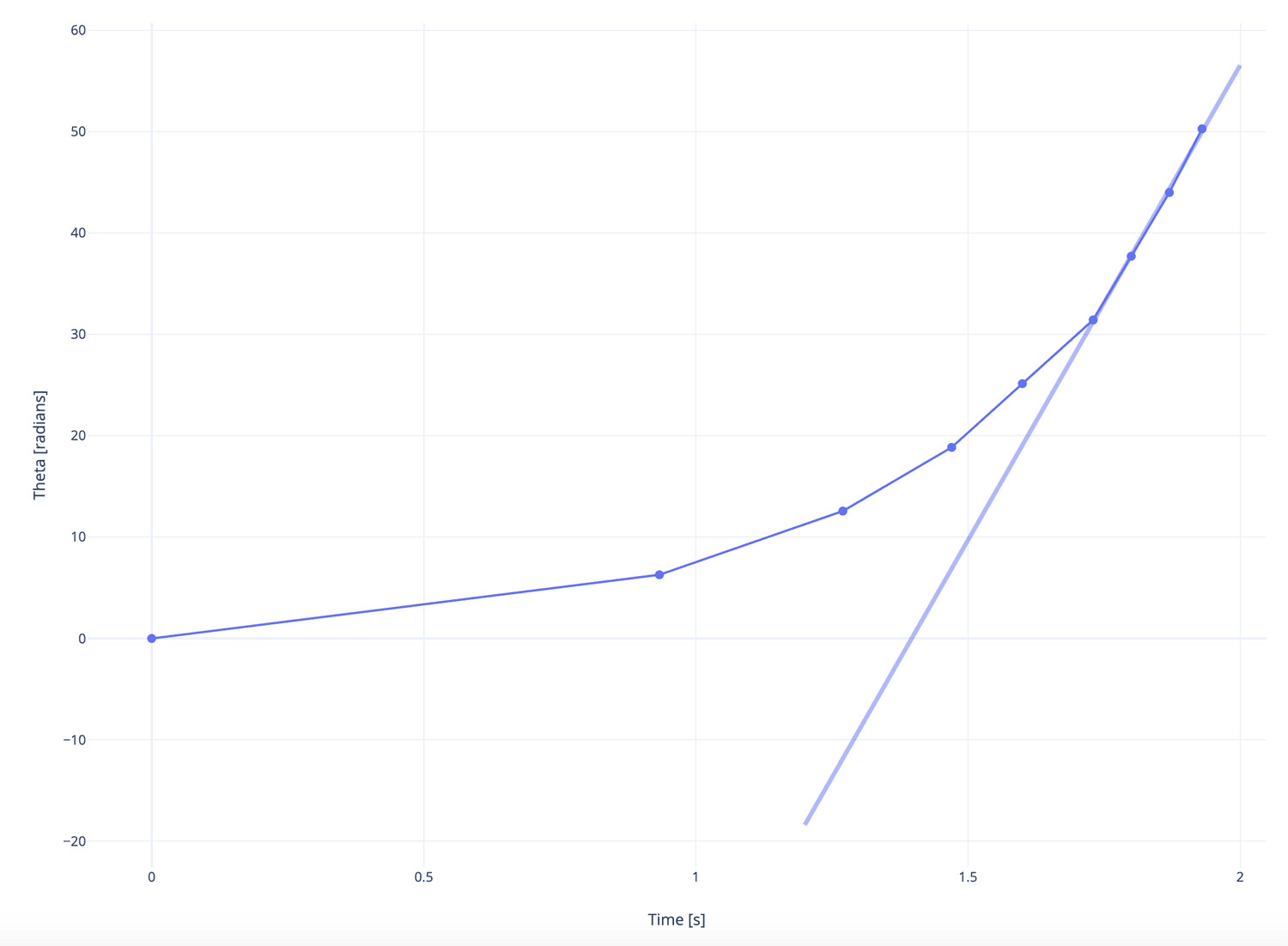
يزداد معدل دوران الذراع مع مرور الوقت، وذلك حتى تصل إلى سرعة مناسبة لقذف الكرة. وإذا نظرنا إلى المخطط السابق، سنجد أن السرعة الزاوية تساوي 93.65 راديان في الثانية.

هناك علاقة بين السرعة الزاوية وسرعة الإطلاق. فإذا تحركت الكرة حركة دائرية (عندما كانت محمولة بواسطة الذراع)، وبنصف قطر قدره r وسرعة زاوية ω، لذا لا بد أن يكون قانون العلاقة بين السرعة الزاوية والخطية صحيحاً:

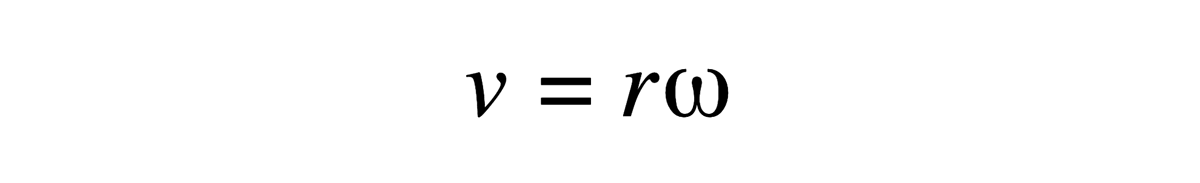
فإذا كان قطر الكرة 21 سم (وهو قطر كرة البولينغ)، والقطر الذي تخلقه الذراع الدوارة 40.5 سم (حصلنا عليه من تحليل الفيديو). لذا ستكون سرعة إطلاق الكرة مساوية لـ42 متر في الثانية –وتلك السرعة أكبر من السرعة المقاسة عن طريق قانون السرعة (المسافة على الزمن). وإذا أُطلقت الكرة بسرعة قدرها 23.85 متر في الثانية (وهي سرعة الإطلاق التي حسبناها سابقاً)، فستملك ذراع الروبوت سرعة زاوية قدرها 53 راديان في الثانية.

القوة اللازمة للإمساك بالكرة وحملها

الآن أصبح لدينا قيمتان لمعدل دوران الذراع، الأولى حسبناها بالاعتماد على سرعة الانطلاق، بينما توصلنا لحساب الثانية عن طريق الموضع الزاوي للذراع. وعلى أي حال، لا تتحرك الكرة (أي كرة كانت) حركة دائرية إلى إذا أثرت عليها قوة ما. وتأتي القوة هنا من أصابع الذراع الحاملة للكرة.

يملك أي جسم يتحرك حركة دورانية تسارعاً، وبما أن التسارع هو معدل تغير السرعة بالنسبة للزمن، وبما أن السرعة هي شعاع، لذا لا بد من وجود تسارعٍ ناتج عن تغير اتجاه الحركة. وتعتمد قيمة هذا التسارع على معدل الدوران وقطر الدائرة التي ترسمها الذراع أثناء حركتها. وبالتالي يمكننا حساب التسارع كما يلي:

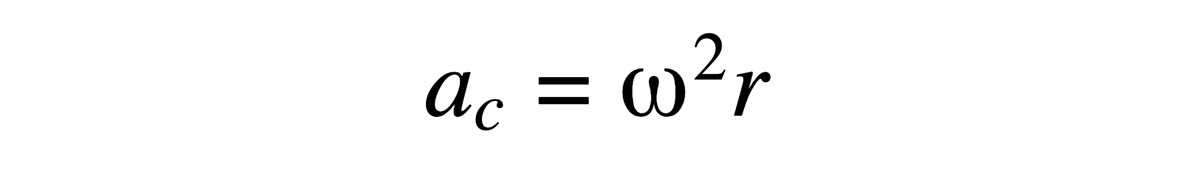
إذاً، كيف نجعل جسماً ما يتسارع؟ بسيطة، نطبق عليه قوة ما. وفي هذه الحالة، لا بد أن تكون هذه القوة هي نفسها القوة التي تدفع الكرة إلى مركز الدائرة لتزيد من سرعتها. وتعتمد هذه القوة على التسارع والكتلة، ويمكن حسابها كالتالي:

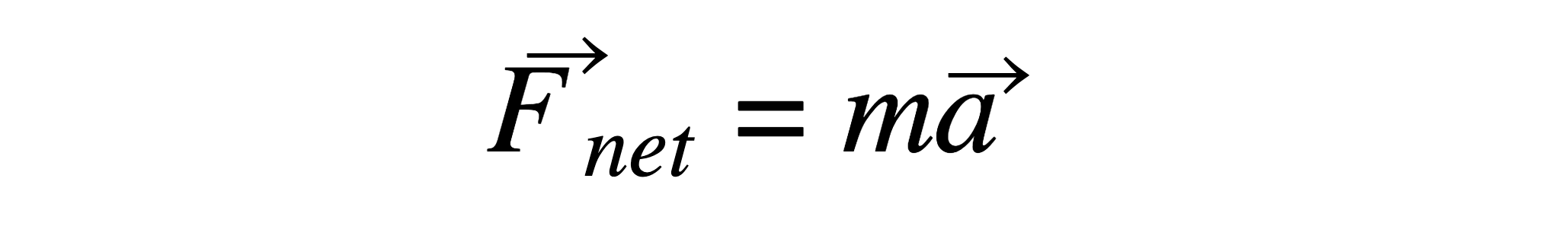
يمكننا حساب التسارع بالاعتماد على قيم السرعة الزاوية التي أوجدناها، ويمكننا تقدير كتلة الكرة بـ 4.5 كغ (10 باوندات). ستطلب هذه المعطيات أن تكون قوة الذراع إما 1138 نيوتن أو 3552 نيوتن (لأننا حصلنا على قيمتين للسرعة الزاوية حسب طرق القياس).

وإذا أخذنا القيمة الأصغر، سنجد أنها قيمة كبيرة جداً، وحتى لو كان للروبوت قوة أكبر مما يستطيع الإنسان تخيله، لكن في حالتنا هذه، لا يطبق الروبوت سوى قوى احتكاك.

وإليكم هذا السؤال، إذا كان معامل الاحتكاك الاستاتيكي بين الكرة وأصابع ذراع الروبوت يساوي 0.8، فما مقدار القوة المطلوب تطبيقها للإمساك بالكرة؟ نتمنى أن تحل هذا السؤال لوحدك.

أسئلة أخرى:

إذا كنت من محبي الفيزياء، فيمكنك الاستمتاع بهذا الفيديو جداً، إليك بعض الأشياء الأخرى التي يمكننا حسابها:

• ماذا سيحدث لو قُذفت الكرة بعد زمن (أو قبل زمن) قدره 0.01 ثانية من زمن قذفها الأصلي، وكم سيغير هذا التأخر (أو التقديم) من المسافة التي ستقطعها الكرة؟
• وبالحديث عن إطلاق الكرة، هل لاحظت في الفيديو أن الكرة تُقذف في أعلى نقطة لها من الحركة الدائرية؟ أي يجب (في هذه الحالة) أن تُقذف الكرة إلى الأعلى بعيداً جداً عن القطع الخشبية ومضمار البولينغ!
• إذا حسبت الطاقة الحركية للكرة والزمن الذي تستغرقه للوصول إلى سرعة الدوران القصوى، ما الطاقة المطلوبة (مُقاسة بالواط) للحصول على ذلك؟
• هل من المنطقي تجاهل مقاومة الهواء واعتبارها مهملة في هذه الحالة؟
• احسب القوة اللازمة لإبقاء الروبوت ملتصقاً بالأرض أثناء إطلاقه الكرة.

إذاً، هل الفيديو مزيف وغير حقيقي؟

إن إحدى طرق تزييف الفيديو هي أن تصور فيديو حقيقي، ثم تضيف إليه المؤثرات الخاصة. والأسهل من هذا كله أن تُعدل على الفيديو وتضيف إليه المؤثرات الخاصة إذا كان مصوراً عن طريق كاميرا موضوعة على حامل ثلاثي. فالكاميرا المحمولة مثلاً قد تهتز ولو قليلاً، لكن الكاميرا الموضوعة على حامل ستكون ثابتة. ومع ذلك، يمكنك إضافة مؤثرات خاصة كاهتزاز بسيطٍ مزيف.

ونعتقد أن هذا ما حصل في الفيديو السابق. عثرنا على مخطط للحركة في الخلفية للفيديو السابق، وكانت النتيجة كالتالي:

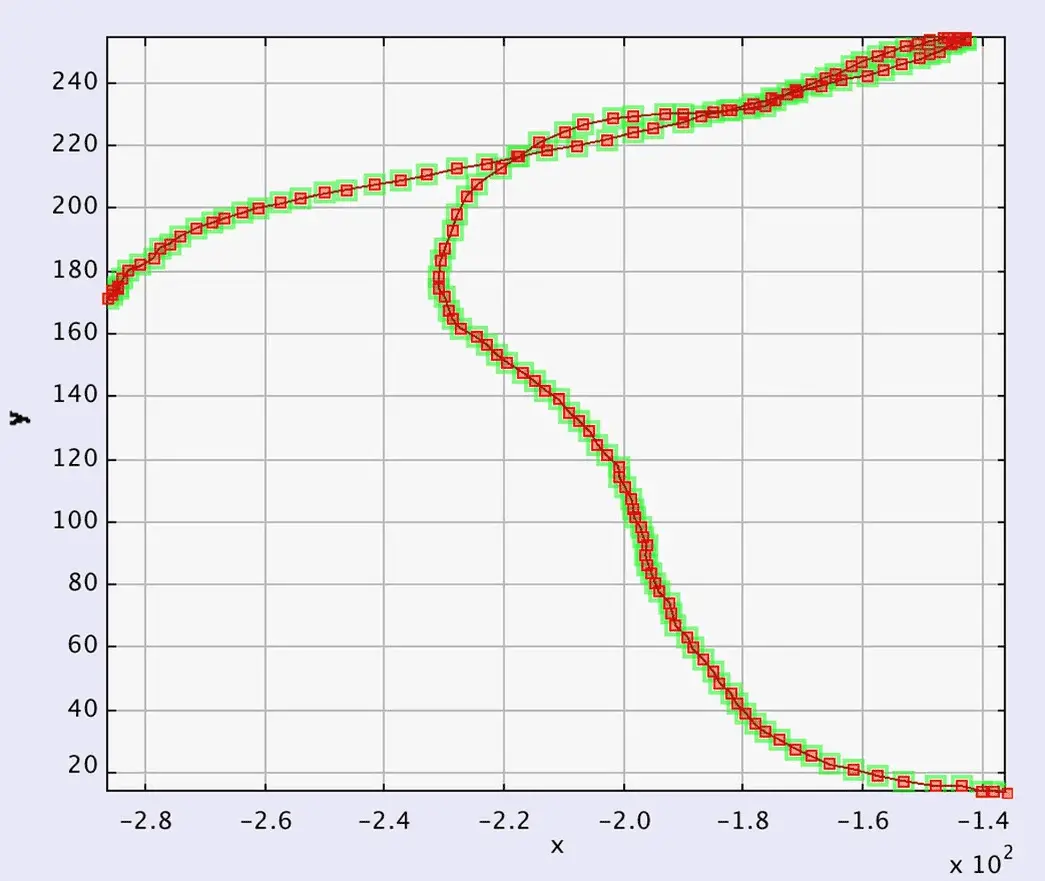
لكن، ماذا سيحدث لو أعدت تصوير الفيديو السابق لكن بكاميرا محمولة على اليد. ستحصل على مخطط كالتالي:

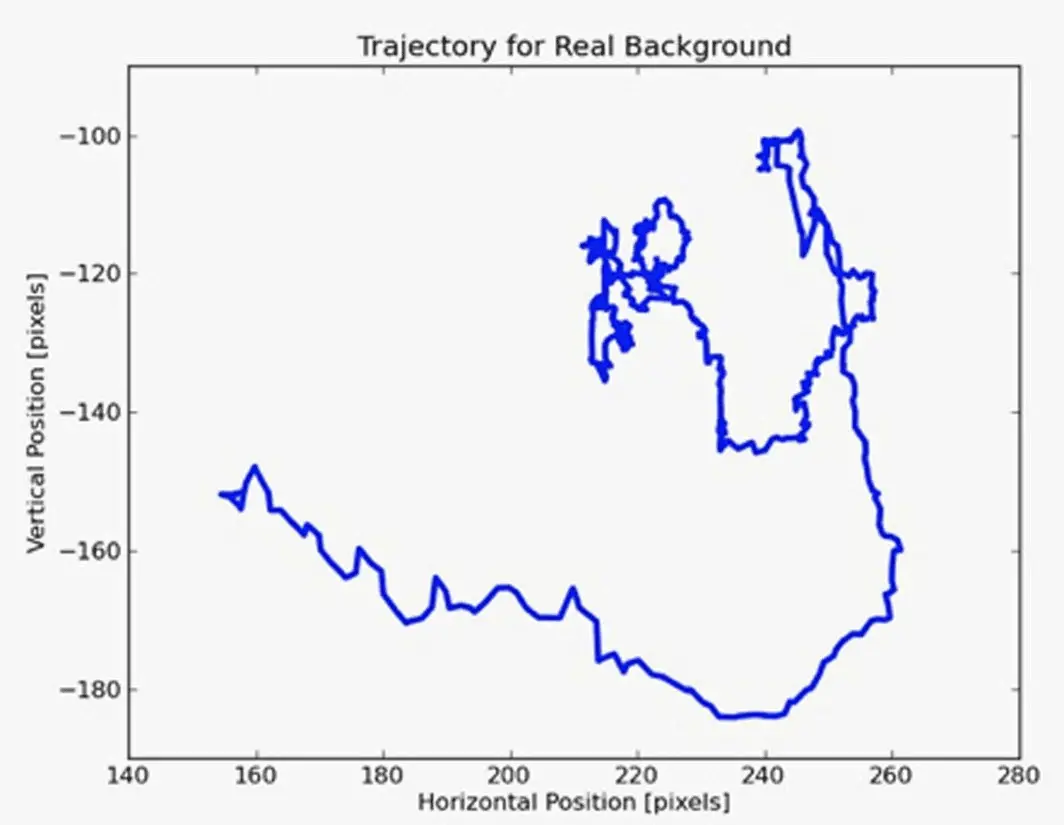
في الواقع، يكون اهتزاز الكاميرا الحقيقة أكثر عشوائية من ذلك، ولن تحصل على مخطط سلس كهذا. لكن من المعقول أن يقوم صاحب الفيديو بتعديل اهتزاز الكاميرا عن طريق برامج معينة لجعله سلساً كالذي رأيناه، ومع ذلك، لا يزال هذا الاهتزاز غير طبيعي (سواء كان مضافاً على الفيديو أم معدلاً على البرامج كي يبدو سلساً).

وعلى أي حال، بصرف النظر عن الفيديو وهل هو مزيف وغير حقيقي أم لا، لا نعتقد أن بناء روبوت كهذا سيكون مشكلة في المستقبل القريب.