دخلك بتعرف معضلة الجريان المضطرب؟ أقدم مسألة لم تحل في الفيزياء

في عام 1932 نال (فيرنر هايزنبرغ) جائزة نوبل لمساهمته في تأسيس مجال ميكانيكا الكم واكتشاف بعض المبادئ الأساسية مثل تفسير كوبنهاجن ومبدأ اللايقين، وتحكي قصة قوله ذات مرة أنه إذا سُمِح له أن يسأل الله سؤالين فسيكونان: ”لماذا خلق ميكانيكا الكم؟ وما هو الجريان المضطرب؟“، وأرجح أنّ الله سيكون قادراً على الإجابة على السؤال الأول.

قد يكون الاقتباس ملفقاً وهناك نسخ مختلفة منه إلا أن (هايزنبرغ) قد صارع وعانى من معضلة الجريان المضطرب لعدة سنوات. قام (أرنولد سومرفيلد)، مشرف الدكتوراه التي كان يُعدها (هايزنبرغ)، بتعيين معضلة الاضطراب له لأنه لم يعتقد أن أياً من طلابه الآخرين كانوا على مستوى التحدي، غير أن مهارات (هايزنبرغ) الهائلة في الرياضيات، والتي سمحت له بالتقدم خطوات جريئة في مجال ميكانيكا الكم، لم توفر له سوى نجاح جزئي ومحدود مع هذه المسألة.

بعد حوالي 90 سنة؛ لا تزال الجهود المبذولة لفهم هذه الظاهرة والتنبؤ بها ذات أهمية عملية هائلة، فهي تشكل الأساس في تصميم الكثير من تقنياتنا، من الطائرات إلى خطوط التوصيل بالأنابيب، وهي تساهم في التنبؤ بالظواهر الطبيعية الهامة مثل الطقس، ولكن نظراً لأن فهمنا لها ظل محدوداً إلى حد كبير ومحصور، فإن تطور التقنيات التي تقوم على تدفقات السوائل اضطر إلى أن يكون بطيئاً وتدريجياً لفترة طويلة، وإذا أصبحنا قادرين على فهم هذه الظاهرة الموجودة في كل مكان، فقد نملك القدرة في تطوير تقنيات كثيرة بطرق أكثر إبداعاً وحرية.

تعريف ما هو غير معرّف:

للأسف مازال الفيزيائيون لا يوافقون على طريقة تعريف موحدة للجريان المضطرب، وهنا سنتكلم عنه كفكرة عامة ونحاول جعلها أكثر دقة مع الوقت، والفكرة العامة هي أن الجريان المضطرب ينطوي على الحركة المعقدة والفوضوية للسائل، والمراد بـ”السائل“ في الفيزياء هو أي شيء يتدفق، بما في ذلك السوائل والغازات، وأحياناً المواد الدقيقة مثل الرمل.

الجريان المضطرب في كل مكان حولنا، لكنه عادة ما يكون غير مرئي. ما عليك سوى تلويح يدك أمام وجهك وقد قمت بإنشاء تغيرات معقدة لا حصر لها في الجو، حتى لو لم تتمكن من رؤيتها. عادة ما تكون حركة السوائل خفية إلا عند مراقبة السوائل التي لها خصائص بصرية مختلفة، فيمكنك رؤية الدوامات على سطح جدول متدفق على سبيل المثال ولكن ليس أنماط الحركة تحت السطح.

يرتبط تاريخ التقدم في فهم ديناميكا الموائع ارتباطاً وثيقاً بالتقنيات الاختبارية القادرة على تصوير التدفق، لكن قبل وقت طويل من ظهور التقنيات الحديثة لأجهزة استشعار التدفق والفيديو عالي السرعة، كان هناك أولئك المفتونون بتنوع وتعدد أنماط التدفق المعقدة.

ولكي يعتبر الاضطراب مشكلة قابلة للحل في الفيزياء نحتاج لأن نكون قادرين على إثبات أننا نستطيع وضع المعادلة الأساسية التي تصف الحركة السائلة ثم حلها للتنبؤ بالتفصيل بكيفية تحرك السوائل تحت مجموعة معينة من الظروف أياً كانت، لكن السبب الرئيسي في أننا لا نستطيع فعل ذلك بشكل عام هو أن العديد من علماء الفيزياء يعتبرون الاضطراب مشكلة لم تحل.

ونقول ”العديد“ لأن البعض يعتقد أنه يجب اعتبارها محلولة، على الأقل من حيث المبدأ. حجتهم هي أن حساب التدفقات المضطربة هو مجرد تطبيق لقوانين نيوتن للحركة حتى وإن كانت معقدة للغاية.

إلا أن هنالك من يرفض هذا القول، وقد أدى عدم وجود نظرية كاملة مُرضية مستندة إلى الفيزياء الكلاسيكية إلى وجود اقتراحات بأن الحساب الكامل للجريان المضطرب يتطلب بعض عناصر الميكانيكية الكمومية: وهي وجهة نظر الأقلية، ولكن لا يمكن استبعادها.

ملاحظة للفيزيائيين والمهندسين:

سنستخدم كلمة تدفق و جريان للدلالة على الشيء نفسه، وكلمة ”السرعة“ في هذه المقالة كدلالة لعدد (رينولدز) الذي هو مزيج من السرعة وقياس الطول واللزوجة التي تحدد نوع التدفق، بما في ذلك ما إذا كان ينبغي لنا أن نتوقع حدوث اضطراب، ولكن إذا كنت تضع العوامل الأخرى ثابتة، فهي تتناسب مع سرعة التدفق.

من الأمثلة على أن الاضطراب مشكلة لم تحل بعد هو أننا لا نستطيع أن نتنبأ بشكل عام بالسرعة التي سيقوم بها التدفق المنظم غير المضطرب بالتحول إلى تدفق مضطرب، رغم أنه يمكننا أن نتوقعها بشكل جيد في بعض الحالات الخاصة –كانت هذه إحدى المشكلات التي حقق فيها (هايزنبرغ) بعض النجاح–

هناك العديد من الظواهر في الطبيعة التي توضح التحول المفاجئ من تدفق هادئ ومنظم في كثير من الأحيان إلى جريان مضطرب، وهنالك ظاهرة أخرى مألوفة لكل من يتردد على الشاطئ، فكر في أمواج المحيط المتموجة والمرتفعة التي تصبح معقدة التموج وأشبه برغوة عند اقترابها من الشاطئ وكيف ”تنكسر“. يمكن أيضاً للأمواج التي تتحرك بفعل الرياح في المحيط المفتوح أن تنكسر إذا كانت سرعة الرياح عالية أو إذا تجمعت موجات متعددة لتشكل واحدة أكبر.

كمثال مرئي آخر، هناك رسم ياباني مشهور يرجع إلى قرون من الزمن يصوّر الجريان المضطرب وانكسار أمواج المحيط:

بدا هؤلاء الفنانون مهتمين بشكل أساسي بنقل الجمال والقوة الرهيبة لهذه الظاهرة، وأحد أشهر الأعمال الفنية اليابانية، والمثال الأيقوني لهذه التجسيدات، هو «الموجة العظيمة» للفنان (كاتسوشيكا هوكوساي)، وهي لوحة مرسومة على الخشب ظهرت في عام 1831.

هنالك سبب أخير لاعتبار الجريان المضطرب مشكلة غير محلولة، وهو أن التدفقات المضطربة تظهر مجموعة واسعة من السلوكيات المثيرة للاهتمام في الزمان والمكان، تم اكتشاف معظمها بالقياس ولم يتم التنبؤ بها، ولا يوجد تفسير نظري مُرضي لها.

المحاكاة:

لماذا يُعد الجريان المضطرب صعب الحل للغاية؟ تأتي أفضل إجابة من خلال النظر إلى التاريخ والبحث الحالي لما وصفه (ريتشارد فاينمان) ذات مرة بأنه ”أكبر مشكلة غير محلولة في الفيزياء الكلاسيكية“.

الصيغة الأكثر شيوعاً لوصف تدفق السوائل هي معادلات (نافييه-ستوكس)، وهي معادلات غير خطية تصف حركة الموائع النيوتونية، تحصل عليها إذا قمت بتطبيق قانون نيوتن الثاني للحركة F = ma (القوة = الكتلة × التسارع) على السوائل ذات خصائص المواد البسيطة، ولا تنجح عند صياغة حل بدقة لتدفقات الطلاء والبوليمرات وبعض السوائل البيولوجية مثل الدم (هناك العديد من المواد الأخرى التي لا تتوافق مع معادلات نافييه-ستوكس)، ولكن بالنسبة للماء والهواء والسوائل والغازات البسيطة الأخرى، فإنها تعد تقريباً صيغة ممتازة.

من الصعب حل معادلة (نافييه-ستوكس) لأنها معادلة غير خطية، وهذا يعني شيئاً محدداً: إذ يمكنك إيجاد حل معقد لمعادلة خطية عن طريق إضافة العديد من الحلول البسيطة، أحد الأمثلة هو الصوت: فمعادلة الموجات الصوتية خطية لذا يمكنك بناء صوت معقد من خلال الجمع بين العديد من الأصوات البسيطة للترددات المختلفة (نغمات متوافقة). ميكانيكا الكم الأولية خطية أيضاً، حيث تسمح لك معادلة (شرودنغر) بإيجاد عدة حلول معاً لإيجاد حل جديد.

غير أن ديناميكيا الموائع لا تعمل بهذه الطريقة، حيث أن عدم خطية معادلات (نافييه-ستوكس) يعني أنك لا تستطيع بناء الحلول عن طريق إضافة حلول أبسط معاً، هذا جزء مما جعل عبقرية (هايزنبرغ) الرياضية تخضع لمثل هذا الاختبار الصعب فيما يخص الجريان المضطرب، حينها أُجبر (هايزنبرغ) على إجراء تقديرات وافتراضات عدة بغية تحقيق أي تقدم في أطروحته، لكن كان من الصعب تفسير بعضها. على سبيل المثال، أثار عالم الرياضيات التطبيقية (فريتز نوثر) –شقيق (إيمي نوثر)– اعتراضات بارزة على حسابات (هايزنبرغ) للجريان المضطرب لمدة عقود قبل أن يعترف في النهاية أنها تبدو صحيحة بعد كل شيء. (كان الموقف صعباً جداً لدرجة أن (هايزنبرغ) نفسه قال، وهو يعتقد أن طريقته مبررة، أنه لم يستطع العثور على الخلل في منطق (فريتز نوثر) أيضاً!)

أما المعادلات المشابهة لـ(نافييه-ستوكس) التي تستخدم لوصف السوائل الأكثر تعقيداً فهي أيضاً غير خطية، كمعادلة (أويلر) التي تحذف آثار الاحتكاك، فهناك حالات حيث يعطي التقريب الخطي نتائج جيدة عند الجريان بسرعات بطيئة للغاية (جريان العسل من الجرة مثلاً)، ولكن هذا لا يشمل معظم الحالات ذات الاهتمام بما في ذلك الجريان المضطرب.

ديناميكا الموائع الحاسوبية:

على الرغم من شبه استحالة العثور على حلول رياضية لمعادلات لتدفق السوائل في ظروف واقعية، فإن العلم مازال بحاجة للحصول على نوع من القدرة التنبؤية للجريان المضطرب، لهذا تحول العلماء والمهندسون إلى الخيار الوحيد المتاح عندما أخفق قلم الرصاص والورق: إلى ”الحاسوب“، حيث يحاولون تحقيق الاستفادة القصوى من الأجهزة الحديثة لتخفيف حدة صعوبة إحدى التطبيقات الأكثر تطلباً للحوسبة العددية: حساب التدفقات المضطربة.

وقد انتفعت الحاجة لحساب هذه التدفقات الفوضوية من تحسين الأساليب الرقمية وأجهزة الكمبيوتر منذ ظهور أول الأجهزة العملاقة، ويسمى هذا المجال ديناميكيا الموائع الحاسوبية، وعادة ما يتم اختصارها بـCFD.

طبق المهندسون والعلماء في وقت مبكر من تاريخ CFD تقنيات رقمية بسيطة من أجل محاولة التقريب المباشر لحلول معادلات (نافييه-ستوكس)، وهذا ينطوي على تقسيم المكان أو المساحة إلى شبكة من الخطوط المتقاطعة وحساب متغيرات السوائل (الضغط والسرعة) عند كل نقطة في هذه شبكة.

غير أن مشكلة النطاق الواسع من المقاييس المكانية تجعل هذا النهج صعباً: فستحتاج إلى إيجاد حل تكون فيه خصائص التدفق دقيقة بالنسبة لأكبر المقاييس، كالمتر للمواسير وآلاف الكيلومترات بالنسبة للطقس وصولاً إلى المقياس الجزيئي، حتى إذا قمت بتقليص المقياس الطولي لميليمترات أو سنتمترات، فستظل بحاجة إلى ملايين النقاط في الشبكة.

هنالك نهج واحد للحصول على دقة معقولة بشبكة بحجم معقول، ذلك بإدراك أنه غالباً ما توجد مناطق كبيرة حيث لا يحدث فيها الكثير من الجريان، بعبارة أخرى، في المناطق البعيدة عن الأجسام الصلبة أو الاضطرابات الأخرى من المرجح أن يتغير التدفق ببطء في المكان والزمان وستكون كل الحركة مركزةً في مكان آخر، والمناطق المضطربة توجد عادة بالقرب من الأجسام أو الأسطح.

إذا ألقينا نظرة على الجناح الحامل، أو ”الجنيّح“، في الطائرة وتخيلنا تدفقاً منتظماً يبدأ من اليسار ويمر من الأعلى فيمكن أن يكون من الأكثر فعالية تركيز نقاط الشبكة بالقرب من الجسم، خاصة عند الحواف الأمامية والخلفية، وليس نقاط الشبكة ”الضائعة“ البعيدة عن الجناح.

هذا هو أبسط أنواع الشبكات ثنائية الأبعاد غير المنتظمة التي لا تحتوي إلا على خطوط مستقيمة. تُسمى حالة الشبكات غير المنتظمة التحسين الشبكي المتكيف AMR، حيث تتغير الخطوط المتقاطعة –أو الشبكة– وتتكيف مع التدفق أثناء المحاكاة، ما يُركز على نقاط الشبكة التي هناك حاجة لها وليس إهدار النقاط في مناطق ذات تدفق منتظم تقريباً.

يهدف البحث في هذا المجال إلى تحسين عملية توليد الشبكات مع تقليل التأثيرات الاصطناعية للشبكة على المادة المدروسة، وهنا صورة لمحاكاة أجرتها ناسا للتدفق حول شفرة دوارة تتأرجح تمثل الاضطراب الدوامي، وهو متعلق بالزخم الزاوي.

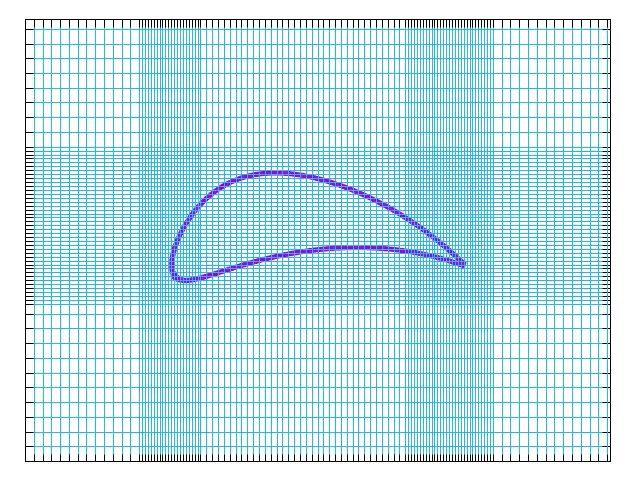
توضح الصورة أعلاه الشبكة المحوسبة التي تظهر على هيئة خطوط زرقاء بالإضافة إلى الجناح الحامل والمادة المتدفقة، وتوضح كيف تتكيف الشبكة مع التدفق. (تكون نقاط الشبكة قريبة من بعضها البعض في المناطق ذات دقة الشبكة الأعلى حيث تظهر كمناطق زرقاء كثيفة)، وعلى الرغم من القدرات التي اكتسبتها الشبكات التكيفية إلا إن عمليات المحاكاة المشابهة لا تزال صعبة من الناحية الحسابية، حيث يستهلك حساب من هذا النوع 2000 نواة حسابية لمدة أسبوع تقريباً.

قام (ديمتري مافريبليس) ومعاونوه في مختبر Mavriplis CFD في جامعة (وايومينغ) بإتاحة العديد من مقاطع الفيديو لمحاكاة AMR التي قاموا بها، وأدناه إطار من شريط فيديو لمحاكاة تدفق على جسم. يعتبر الفيديو مفيداً للحصول على فكرة عن كيفية عمل تقنية AMR لأنه يوضح كيفية تتبع الشبكة الحسابية لميزات التدفق.

عملهم هو مثال على قدرة التقنيات العددية الحديثة على التقاط جزء من آلية الانتقال لحالة الاضطراب موضحة في صورة الهواء المسخن بالشموع أعلاه، كما أن هنالك نهجاً آخر للحصول على أقصى استفادة من موارد الحاسوب ينطوي على إجراء تعديلات على معادلة الحركة، بدلاً من/أو بالإضافة لتغيير الشبكة المحوسبة.

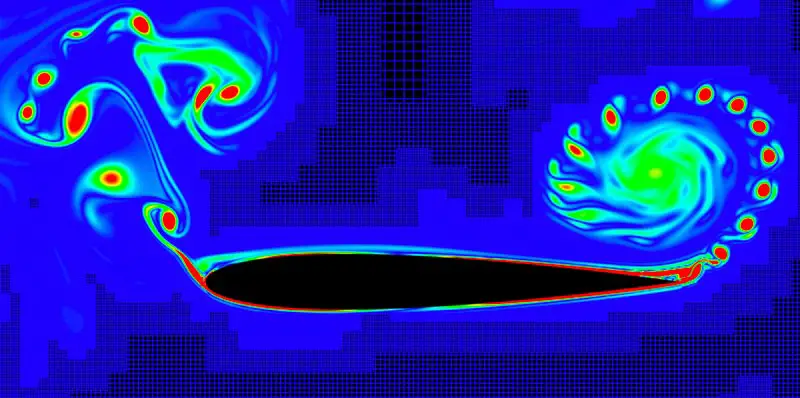
منذ أن بدأت المحاكاة العددية المباشرة الأولى لمعادلات (نافييه-ستوكس) في مختبر (لوس ألاموس) الوطني في أواخر الخمسينات من القرن العشرين، جرت مواجهة مشكلة النطاق الواسع من المقاييس المكانية مع بعض أشكال نمذجة التدفق للمقاييس الصغيرة. بمعنى أنه تم حل معادلات (نافييه-ستوكس) الفعلية للحركة على المقاييس المتوسطة والكبيرة، ولكن ببعض الاقتطاع واستبدال نموذج إحصائي بآخر.

الفكرة هي أن الديناميكيات المثيرة للاهتمام والمهمة تحدث على المقاييس الأكبر، وهنا يأتي دور نقاط الشبكة الأهم، لكن الحركات الشبكية القرعية التي تحدث بين نقاط الشبكة هي تبدد للطاقة فقط، أو تحول الحركة إلى حرارة، لذا لا يلزم تتبعها بالتفصيل، ويطلق على هذه الطريقة محاكاة كبيرة الحجم LES، وهي تختص بالتدفقات على مقياس طولي معين.

هناك العديد من الطرق البارزة الأخرى لنمذجة تدفقات السوائل على أجهزة الكمبيوتر، وبعضها لا يستخدم الشبكات على الإطلاق، ولعل أكثرها نجاحاً هو التقنية المسماة ”تقنية حركية الموائع للجسيمات الملساء“ SPH، والتي، كما يوحي اسمها، تقوم بتجميع السوائل كمجموعة من ”الجسيمات“ الحسابية التي يتم تحريكها بدون استخدام الشبكة. تأتي كلمة ”ملساء“ في الاسم من الاختلاط السلس بين الجسيمات التي تستخدم لاشتقاق خصائص السائل في نقاط مختلفة في الفضاء.

النظرية والاختبار:

على الرغم من القدرة المثيرة للإعجاب (والمتطورة باستمرار) لعلماء ديناميكيات السوائل في حساب التدفقات المعقدة بأجهزة الكمبيوتر، ويستمر البحث عن فهم نظري أفضل للجريان المضطرب، لأن أجهزة الكمبيوتر يمكنها حساب حلول التدفق في حالات معينة فقط، وحالة واحدة في كل مرة.

وفقط من خلال استخدام الرياضيات، يشعر الفيزيائيون أنهم حققوا فهماً عاماً لمجموعة من الظواهر ذات الصلة، ولحسن الحظ هناك عدد من الطروح النظرية الرئيسة للجريان المضطرب، كل منها يحوي بعض الظواهر المثيرة للاهتمام التي يُسعى إلى تفسيرها.

لا يُعرف سوى عدد قليل من الحلول الدقيقة لمعادلات (نافييه-ستوكس)، تلك التي تصف الجريان الصفيحي البسيط (وبالتأكيد ليست تدفقات مضطربة من أي نوع)، مثل التدفق في ماسورة أو بين لوحين مسطحين، فتكون سرعة التدفق بين لوحين صفر عند الأطراف وقصوى في منتصف المسافة بينهما. هذا التدفق المكافئ (كما هو موضح أدناه) محلول بالمعادلات، وهو معروف منذ أكثر من قرن، فالتدفق الصفيحي في الأنبوب متماثل بسرعة عظمى في المركز.

الشيء المثير للاهتمام حول هذا الحل المكافئ، والحلول الدقيقة المماثلة، هو أنه صالح (من الناحية الحسابية) عند أي سرعة تدفق مهما كانت عالية، ومع ذلك تظهر التجربة أن هذا ينجح بسرعات منخفضة، إلا أنّ التدفق يتفكك ويصبح مضطرباً عند بعض السرعات ”الحرجة“، واستخدام الأساليب الرياضية لمحاولة العثور على هذه السرعات الحرجة هو جزء مما كان يعمل عليه (هايزنبرغ) في أطروحته.

يصف الباحثون ما يحدث هنا باستخدام لغة نظرية الاستقرار، ونظرية الاستقرار هي دراسة الحلول الدقيقة لمعادلة (نافييه-ستوكس) وقدرتها على تجاوز الاضطرابات الصغيرة التي تضاف إلى التدفق. يمكن أن تكون هذه الاضطرابات على شكل حدود مادية (وسط) أقل سلاسة، أو تغيرات في الضغط الذي يدفع التدفق، إلخ.

الفكرة هي أنه عندما يكون هنالك حل صالح لسرعة منخفضة، فإنه بالقرب من السرعة الحرجة يصبح هنالك حل آخر صالح أيضاً، وبالطبع يتم تفضيل الحل الثاني الأكثر تعقيداً. بعبارة أخرى: أصبح الحل البسيط غير مستقر فيتم استبداله بواحد آخر، ومع زيادة السرعة أكثر يفسح كل حل الطريق أمام حل أكثر تعقيداً حتى نصل إلى التدفق الفوضوي الذي نسميه الجريان المضطرب.

في العالم المادي هذا ما سيحدث على الدوام لأن الاضطرابات موجودة دائماً، وهذا هو السبب في أن الجريان الصفيحي أقل شيوعاً من الاضطراب في الحياة اليومية، حيث أنها أكثر تعقيداً.

التجارب اللازمة لمراقبة حالات عدم الاستقرار هذه مباشرةً دقيقة جداً لأن المسافة بين عدم الاستقرار الأول وبداية الاضطراب الكامل تكون عادة صغيرة للغاية، يمكنك رؤية العملية في الشكل السابق حيث يظهر الانتقال إلى الجريان المضطرب في عمود الهواء الساخن فوق الشمعة فجأة تقريباً، إذ إن العمود المستقيم غير مستقر ولكن الأمر يستغرق بعض الوقت قبل أن يتحول عدم الاستقرار المتعرج لدرجة يمكن ملاحظته كتذبذب مرئي، وفي الوقت الذي يحدث فيه هذا تتكدس سلسلة من حالات عدم الاستقرار ونشهد تحولاً مفاجئاً لحالة الجريان المضطرب.

مثال آخر في الرسم التوضيحي التالي الذي يبين الانتقال النموذجي إلى الاضطراب في تدفق يحده جدار واحد.

يمكننا أن نرى مرة أخرى اضطراباً شبه دوري للتدفق الصفيحي يبدأ في الظهور، وبعد عدد قليل من الأطوال الموجية يصبح التدفق فجأة مضطرباً. يشكل التحول إلى الاضطراب والتنبؤ به تحدياً مستمراً للمحاكاة والنظرية، وعلى الجانب النظري يبدأ العمل بنظرية الاستقرار.

في تدفقات السوائل القريبة من الجدار، يمكن أن يسلك الانتقال إلى الاضطراب شكلاً مختلفاً إلى حد ما، وكما هو الحال في الأمثلة الأخرى الموضحة يتم تضخيم الاضطرابات الصغيرة بالتدفق حتى تتحول إلى حركة فوضوية مضطربة، لكن الاضطراب لا يشمل السائل بأكمله بل يحصر نفسه في بقع معزولة محاطة بتدفق صفيحي خفيف، في النهاية سيكون هناك المزيد من البقع التي تتطور وتتزايد وتندمج حتى يصبح التدفق بأكمله مضطرباً.

الشيء المثير في هذه البقع هو أنه، بطريقة ما، يمكن أن يدخلها السائل ويخضع لحركة فوضوية معقدة ويخرج بهدوء كتدفق منظم غير مضطرب على الجانب الآخر. في الوقت الذي تستمر فيه البقع كما لو كانت أجساماً مغمورة بالتدفق ومحدودة مادياً.

على الرغم من تعاقب العقول الرياضية التي أثارتها معادلات (نافييه-ستوكس) منذ أن وُضعت قبل ما يقرب قرنين من الزمن، إلا أن الحلول الدقيقة ما زالت نادرة ومحدودة والأسئلة الأساسية حول المعادلة تبقى دون إجابة، فما زلنا لا نعرف ما إذا كان للمعادلة حلول في جميع الحالات، كما أننا لسنا متأكدين ما إذا كانت حلولها، التي من المفترض أنها تمثل التدفقات الحقيقية للماء والهواء، صالحة على الدوام، أو ما إذا كان بعضها يُفجر طاقات لا نهائية أو غير ممكن فيزيائياً.

فالعالِم الذي يمكنه حل هذه الأمر سيحصّل مليون دولار أمريكي، فهي واحدة من المسائل الرياضية السبعة التي لم تحل في جائزة مسائل الألفية التي وضعها معهد (كلاي) للرياضيات.

لحسن الحظ، هناك طرق أخرى للتعامل مع نظرية الجريان المضطرب، وبعضها لا يعتمد على معرفة الحلول الدقيقة لمعادلات الحركة. تستخدم دراسة إحصائيات الاضطراب معادلة (نافييه-ستوكس) لاستنتاج متوسط ​​خصائص التدفقات المضطربة دون محاولة حل المعادلات بالضبط، وتقوم على أسئلة مثل: ”إذا كانت سرعة التدفق هنا كذا فما هو احتمال أن تكون السرعة التي تبعد سنتيمتراً واحداً في نطاق معين؟“، كما تجيب عن أسئلة حول متوسط ​​الكميات لأشياء مثل المقاومة عند محاولة دفع المياه من خلال أنبوب، أو قوة الرفع على جناح الطائرة، وهذه الكميات هي التي تحوي الأهمية الحقيقية للمهندسين الذين لا يستفيدون إلا قليلاً من الوصوف الفيزيائية أو الرياضية المعقدة.

اتضح أن العقبة الكبيرة الوحيدة في طريقة المقاربة الإحصائية لنظرية الجريان المضطرب هي، مرة أخرى، العبارة غير الخطية في معادلة (نافييه-ستوكس)، فعندما تستخدم هذه المعادلة لاشتقاق معادلة أخرى لمتوسط ​​السرعة في نقطة محددة، فإنها تحتوي على عبارة تتضمن شيئاً جديداً: ارتباط السرعة بين نقطتين.

عندما تقوم باشتقاق المعادلة لعلاقة السرعة هذه تحصل على معادلة بعبارة جديدة أخرى: ارتباط سرعة يتضمن ثلاث نقاط، وهذه العملية لا تنتهي أبداً، حيث تستمر العبارة اللاخطية في إنشاء علاقات ارتباط عالية المستوى.

تُعرف الحاجة إلى إنهاء أو ”إغلاق“ هذه السلسلة غير المحدودة من المعادلات بطريقة ما باسم ”مسألة الإغلاق“ في نظرية الجريان المضطرب، ومازالت موضوعاً للبحث المكثف. باختصار شديد، لإغلاق المعادلات تحتاج للتخلص من الإجراء الرياضي واللجوء إلى افتراض أو تقريب نابع عن حاجة فيزيائية.

على الرغم من الصعوبة، فإن بعض أنواع الحلول الإحصائية لمعادلات الموائع تعتبر أساسية في وصف ظاهرة الجريان المضطرب الكامل. لا يجب أن يكون الجريان المضطرب مجرد امتداد عشوائي غير مألوف لسائل متحرك، وعادة ما يكون أكثر إثارة من ذلك.

واحدة من أكثر الظواهر إثارة للفضول هي وجود هياكل ثابتة ومنتظمة ضمن بيئة تدفق عنيفة وعشوائية، فجميعنا على دراية بالعواصف على كوكب المشتري، المميزة والواضحة بعظمتها من على الكوكب، والتي تستمر لسنوات، فهي جزء لا يتجزأ من حالة جريان مضطرب للغاية، أما على كوكب الأرض فيجب على الخبراء أن يعانوا الكثير إذا أرادوا إنشاء حقل جريان مضطرب متجانس حقاً دون أي بنية مدمجة.

في هذه الصور تظهر حركة مضطربة أخرى بشكل أسطوانة ثم تنتقل إلى جريان مضطرب في تدفق مقيّد، يمكنك رؤية أصداء الاضطرابات المشابهة للموجة التي تسبق بداية الجريان المضطرب الكامل: وهي دورية تستمر حتى يصبح التدفق فوضوياً.

عندما يكون من الصعب جداً حل المعادلة الأساسية أو حتى محاكاتها، فمن الطبيعي أن تبحث عن معادلة أو نموذج أكثر طواعية ولايزال يشمل معظم المبادئ الفيزيائية الهامة، والكثير من العمل النظري لفهم الاضطراب من هذا النوع.

ذكرنا نماذج الشبكة الفرعية التي تستخدم لتقليل عدد نقاط الشبكة المطلوبة في محاكاة عددية، وهناك أسلوب آخر لتبسيط معادلة (نافييه-ستوكس) هو نوع من النماذج يسمى ”نماذج الغلاف“، وتعمل هذه النماذج على «تحويل (فورييه)» لمعادلة (نافييه-ستوكس) مما يؤدي إلى وصف السائل كعدد كبير من موجات متفاعلة بأطوال موجية مختلفة ثم، بطريقة منتظمة، يمكنك تجاهل معظم الموجات مع الحفاظ على حفنة من الموجات المهمة فقط.

يمكنك بعد ذلك حساب، باستخدام الكمبيوتر أو باليد، التفاعلات والخصائص المضطربة الناتجة. في حين أن الكثير من الجوانب الفيزيائية تختفي في هذه الأنواع من النماذج، إلا أنها تسمح بوجود بعض أنواع الخصائص الإحصائية للجريان المضطرب التي يجب دراستها في الحالات التي لا يمكن فيها حل المعادلات بالكامل.

في بعض الأحيان نسمع عن ”نهاية الفيزياء“، وفكرة أننا نقترب من المرحلة التي سيتم فيها الإجابة على جميع الأسئلة المهمة وسوف يكون لدينا نظرية لكل شيء، لكن من وجهة نظر أخرى، حقيقة أن مثل هذه الظاهرة المعتادة والموجودة في كل مكان حولنا، مثل تدفق المياه عبر الأنبوب، لا تزال من نواح كثيرة مشكلة غير محسومة، وهذا يعني أنه من غير المرجح الوصول إلى نقطة يتفق جميع علماء الفيزياء على أنها نهاية وفهم كامل لمجالهم، ولا يزال هناك ما يكفي من الغموض في العالم من حولنا لإبقاء علماء الفيزياء مشغولين في المستقبل البعيد.