دخلك بتعرف «مسارات أويلر» التي استوحاها من خلال نزهاته المسائية في مدينة كونيغسبرغ

في مقالنا هذا على موقعنا «دخلك بتعرف»، سنقدم لك عزيزي القارئ ما يعرف باسم «مسارات أويلر»، ونظرية المخططات، وإشكالية جسر (كونيغسبرغ)، كما سنقدم لك مثالا عن الطريقة التي صادف بها الرياضياتي (ليونهارد أويلر) مجالا جديدا كليا في علوم الرياضيات.

(ليونهارد أويلر) وهو يعبر الجسور السبعة في (كونيغسبرغ):

إن جمال الخروج في نزهة سيرا على الأقدام بدون أي أمر آخر يعكر صفو ذهنك لا ينسدل على ساقيك فقط، بل أن حتى أفكارك تبدأ في التجوال وتسرح هنا وهناك، حيث ينفتح أمامك مجال يجعل من الممكن لك أن تنسى نفسك بشكل كلي في أعماق عقلك الباطن.

في الواقع؛ هذه طريقة عظيمة للبحث عن حلول لإشكاليات تعذر عليك حلها، وقد يكون هذا واحدا من الأسباب الذي يجعل علماء الرياضيات مشهورين على وجه الخصوص بالخروج في نزهات طويلة سيراً على الأقدام، من أجل التأمل في بعض الأفكار التي تجول في أذهانهم.

هنا سنسرد عليك قصة نزهة من هذا النوع وقصة عالم الرياضيات الذي خاضها، وهو العالم السويسري (ليونهارد أويلر)، الذي كان يسير في مدينة (كونيغسبرغ) عندما لاحظ أمرا مثيرا للاهتمام.

قبل أن نناقش الأمر المثير الذي لاحظه (أويلر)، علينا أولا أن نعرف به بإيجاز: يعتبر (ليونهارد أويلر) واحدا من أعظم علماء الرياضيات على الإطلاق إن لم يكن أعظمهم، فقد حقق الكثير من الإنجازات العظيمة في الجبر والهندسة ونظرية الأعداد. إذا كنت تملك بعض وقت الفراغ، ننصحك أن تسلي نفسك بالمطالعة حول قصة حياته.

لنعد إلى موضوعنا الأساسي الآن: كان (أويلر) يتمشى في مدينة (كونيغسبرغ) عندما لاحظ الجسور السبعة التي تتواجد بها. بما أنه كان غالبا ما يخرج في نزهات سيرا على الأقدام بهذا الشكل، تساءل (أويلر) عما إذا كان من الممكن أن يبدأ نزهته من أي مكان في المدينة وأن لا يعبر أيا من جسورها إلا مرة واحدة.

لم يكن مهما بالنسبة له أين ستكون نهاية نزهته، وقد كان هذا المسار بكل تأكيد ليكون أجمل مسار يتخذه في نزهته من الناحية الرياضياتية.

تيمنا به، صرنا اليوم نطلق على هذه المسارات اسم «مسارات أويلر».

بدلا من محاولة تفسير وشرح مخطط الجسور السبعة في مدينة (كونيغسبرغ) في تلك الأزمنة، دعونا نجعل الأمور أوضح قليلا من خلال بعض الصور:

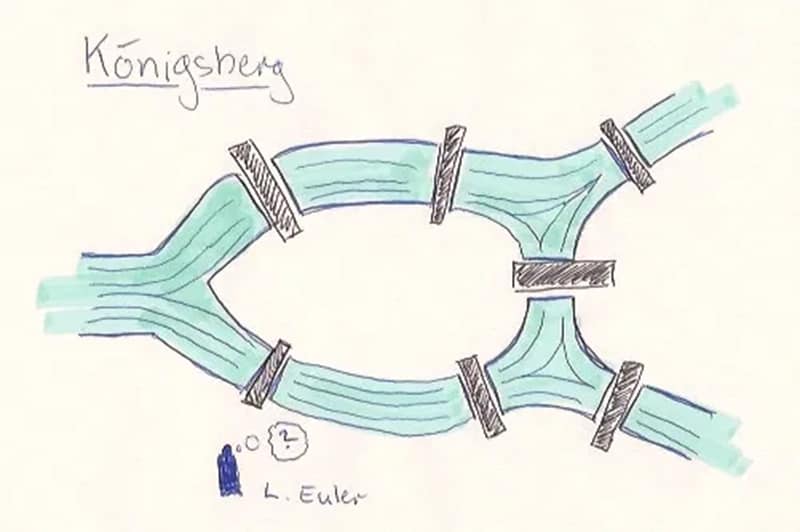
الآن هو الوقت المثالي لمحاولة حلّ هذه المعضلة بنفسك عزيزي القارئ قبل أن تقرأ الحل أسفله.

حاول (أويلر) تماما مثلك عزيزي القارئ بعض الاحتمالات، ووصل إلى استنتاج مفاده أنه لم يكن ممكنا بالنسبة له عبور كل جسر مرة واحدة فقط خلال نزهاته اليومية.

سرعان ما أسرت هذه الإشكالية اهتمامه، وراحت بعض الأسئلة الشائكة تتدفق إلى ذهنه، على شاكلة: لماذا كان عبور كل جسر مرة واحدة مستحيلا؟ هل سيكون الأمر سيانًا مهما كان عدد الجسور؟ هل كان الجواب يعتمد على مخطط الجسور وطريقة توزيعها؟

وهكذا، أصبح دماغه يعج بالأسئلة أكثر من ذي قبل، وكان قد عقد العزم على الإجابة عنها كلها، ونحن هنا لنحذو حذوه.

ترجمة الإشكالية إلى نظرية المخططات:

أولا وقبل كل شيء، من المهم جدا استخلاص المعلومات المهمة والأساسية من المخطط. نحن ننوه إلى أنه لا يهم أي المسارات التي نأخذها على الأرض (غير الجسور)، ومنه لا يجب علينا سوى التركيز على الجسور.

دعونا نعين لكل منطقة أرض ”قمة“ أو ”عقدة“. إذا ما كان هناك جسر من منطقة أرض إلى أخرى نقوم بربط العقدتين بـ”حافة“، وسنستعرض في الصورة رقم 2 خريطة مدينة (كونيغسبرغ) والعقد والحواف التي ذكرناها من قبل.

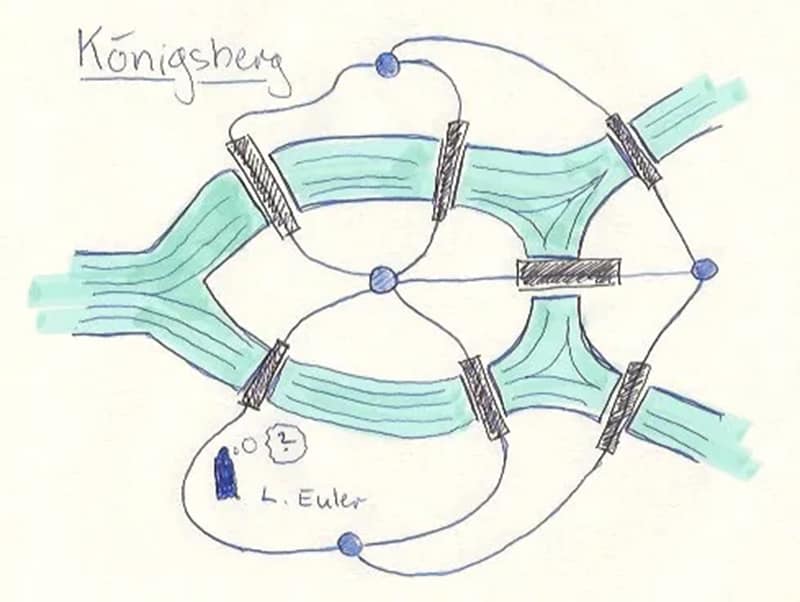
الآن بعدما بتنا نعرف ما يجب علينا التركيز عليه، يمكننا بكل بساطة إزالة الخريطة من الصورة الثانية، والتقيد بالمخطط لوحده، مثلما يظهر في الصورة الثالثة.

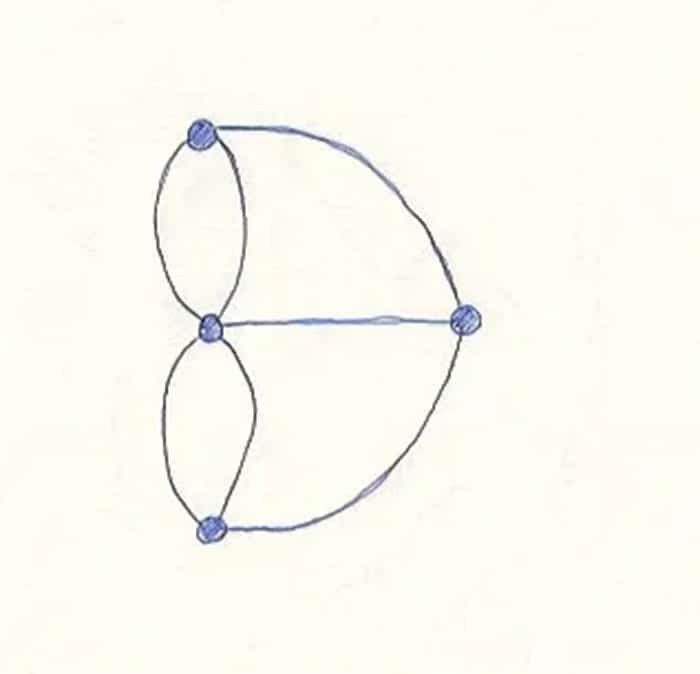
لقد قمنا لتونا بترجمة إشكالية عبور الجسور إلى إشكالية مخطط نظري. أصبحنا الآن نملك جميع المعلومات الضرورية لحل الإشكالية في صورة واحدة، وهي الصورة الثالثة، بدون أية رسومات إضافية غير ضرورية.

نشأة نظرية المخططات:

مثلما ذكرنا أعلاه، نحن في مقالنا هذا نسير على خطى العالم الرياضياتي (أويلر). لحسن الحظ، قادته خطواته إلى هذا الاكتشاف الذي صار يعرف بنظرية المخططات.

إن هذه الإشكالية هي الأولى التي تم ربطها بنظرية المخططات بمعايير اليوم، ومنه تم إنشاء مجال رياضياتي كامل لأن أحدهم لاحظ أمرا غريبًا في حياته اليومية.

من أجل تبسيط الفقرات التي سنتناولها لاحقًا، سيتعين علينا تفسير بعض المفاهيم التي سيتم استخدامها فيها، حيث سنستعمل للدلالة على درجة عقدة ما حرف (ف) وقيمته للدلالة على عدد الحواف المرتبطة بتلك العقدة.

على سبيل المثال، تكون درجة العقدة في أعلى الصورة الثالثة ثلاثة درجات لكل العقد ما عدا العقدة في المنتصف، التي ستكون 5 درجات.

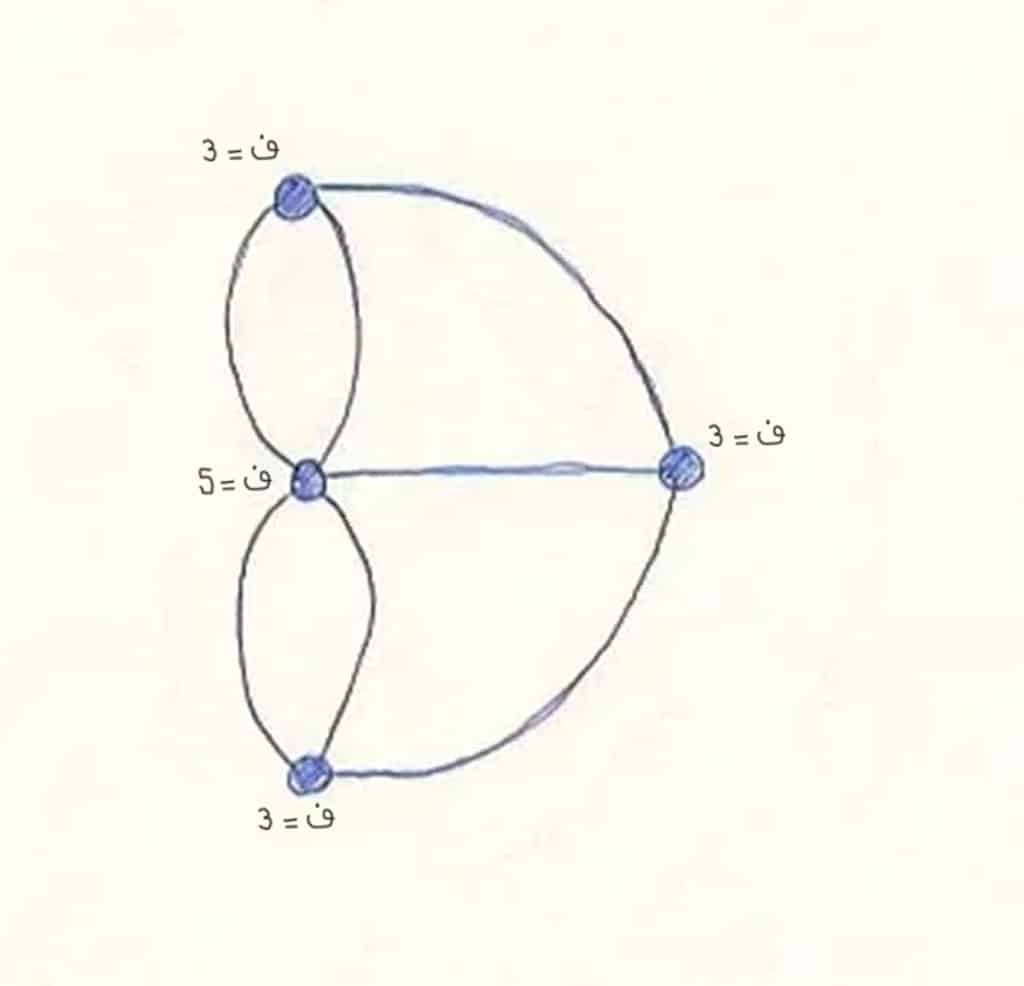
بعد أن تجهزنا بالمفاهيم المناسبة، دعونا نأخذ عقدة لا يمكن اعتبارها نقطة بداية ولا نقطة نهاية لمسار (أويلر) محتمل، فمن البديهي أنه يتعين علينا الوصول إلى هذه العقدة بنفس عدد المرات التي يتوجب علينا مغادرتها فيها، وإن لم تكن هذه هي حال الأمور، فسنجد أنفسنا بصدد التعامل مع نقطة بداية أو نقطة نهاية لمسار (أويلر) محتمل.

ومنه يمكننا اعتبار جميع العقد التي ليست نقاط بداية ولا نقاط نهاية لمسار (أويلر) محتمل عقدًا ذات درجات زوجية.

لنميز بين هاتين الحالتين اللتين يكون في كلتيهما أو إحداهما مسار (أويلر) ممكناً:

1. تكون نقطة البداية ونقطة النهاية هي نفسها (من نقطة أ نحو أ): أي تكون هي نفس العقدة، ومنه لابد لهذه العقدة أن تكون لها عدد درجات زوجي بالضرورة.
2. نبدأ نزهتنا عند العقدة (أ) وننهيها عند العقدة (ب)، حيث (أ) لا يساوي (ب): إذا ما مشينا عبر العقدة (أ) مرة أخرى قبل الوصول إلى العقدة (ب) فلابد لنا من مغادرة العقدة (أ) مرة أخرى، ومنه لابد أن يكون للعقدة (أ) عدد درجات فردي، وبشكل مماثل، سنكون قادرين على إثبات أن (ب) سيكون عددا فرديا هو الآخر.

هذه هي كل الحالات محتملة التي يمكن فيها السير على مسار (أويلر).

نلاحظ أن جميع الرؤوس في الرسم البياني الأخير لها درجة فردية، فلا يمكن أن يكون هناك مسار (أويلر) في هذا الرسم. وهكذا توصلنا إلى نفس النتيجة التي توصلنا إليها (أويلر) ويمكننا أن نستنتج بثقة أنه لم يكن من الممكن التنزه عبر (كونيغسبرغ) وعبور كل جسر مرة واحدة.

في الأخير، الظروف التي قمنا بتأسيسها ضرورية ليتحقق وجود مسار (أويلر) بل هي كافية أيضًا، ففي أي مخطط، يتحقق مسار (أويلر) فقط في حالة ما إذا كانت هناك عقدتين على الأكثر مع درجات فردية (في مثالنا لدينا 4 عقد فردية).

خاتمة:

قام الكثير من المبدعين والمفكرين بتحقيق العديد والعديد من الملاحظات المثيرة وخطرت بأذهانهم أفكار عظيمة من خلال تركهم لأفكارهم تسرح وتجول بحرية بينما يتجولون سيرا على الأقدام.

لا يسع الكثير من الناس اليوم القول بفخر بأنهم شاركوا في نشأة مجال جديد في علوم الرياضيات لأنهم كانوا يتنزهون سيرا على الأقدام، لحسن الحظ، كان العالم الرياضياتي الشهير (أويلر) واحدًا من هؤلاء القلائل، وقد استمتعنا كثيرا بتتبع خطواته وأفكاره في مقالنا هذا.